Gaussian filtering
The usual way to create a Gaussian kernel is to evaluate a Gaussian function at the center of each cell:
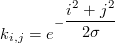
This usually works well, except when the kernel is thin (σ < 1). It gets worse when using our generalised kernel:
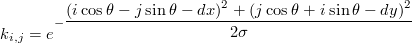
TODO interpolate the Gaussian integral on more points, eg. 5×5 (currently libpipi does it at the central point and at 8 additional points in the neighbourhood).
Code
- browser/libpipi/trunk/pipi/filter/blur.c
- browser/libpipi/trunk/pipi/filter/convolution_template.h
- browser/libpipi/trunk/pipi/filter/convolution.c
Median filtering
There are several ways to optimise a median filter.
The first idea is an approximation, based upon the assumption that the median of subset medians is close to the median of the whole set. It can already be simulated by applying a 5×0 filter and a 0×5 filter instead of a 5×5 filter, so there is no real point in studying this specific optimisation.
The second idea is to optimise the median selection. The most naive method is to bubble-sort the neighbourhood values and select the middle point, which has complexity O(n²) where r is the filter radius and n = (2r+1)². Improving on the sorting algorithm by using eg. heapsort or quicksort, reduces the complexity to O(n.log2(n)). But since we’re only interested in the median and not in ordering the rest of the data, we can use an efficient median selection algorithm. This operation can be done in fewer than 3n tests [1] but the practical implementation is extremely complex.
The third way to optimise a median filter is by accounting for the size of neighbourhood changes in raster scan order: usually only a few values are removed from and added to the list of neighbours. This becomes promising with large kernel sizes, and efficient algorithms exist that handle this case in 1D at least [2].
Today, median filtering methods use O(r) techniques, but O(log(r)) ones exist, too [4].
There is even a method in O(1) [3]. However, like many others, it relies on histograms, which only works well when the input data consists of 8-bit integers. Since libpipi does most of its computations using 32-bit floats, such techniques are of limited usefulness (but should be proposed anyway, because we have ways to tell whether an image has fewer than 8 bits per component).
TODO use ANYTHING but what we currently have... bubble sort, what the fuck!
References
- [1] Uri Zwick, Selecting the median, In Proceedings of the 6rd Annual ACM-SIAM Symposium on Discrete Algorithms (1995)
- [2] Juhola, M. Katajainen, J. Raita, T., Comparison of algorithms for standard median filtering, IEEE Transactions on Signal Processing, Volume 39, Issue 1, Jan 1991 pp. 204-208
- [3] Perreault, S. Hebert, P., Median Filtering in Constant Time, in the September 2007 issue of IEEE Transactions on Image Processing
- [4] Gil, J. Werman, M., Computing 2-D min, median, and max filters, IEEE Transactions on Pattern Analysis and Machine Intelligence, 15, 504-507, 1993
Code
Links
Dilate / erode
Erosion and dilation already work, but only for nearest pixels.
There are techniques to make dilate by X O(1) in infinite distance [1]. Other distances are easily made O(r) with possible optimisations based on kernel symmetry.
TODO each pixel couple test is done twice. There seems to be an opportunity for improvement there.
TODO implement "dilate by X" (Manhattan distance).
TODO implement "dilate by X" (euclidian distance).
TODO implement "dilate by X" (infinite distance).
Code
Links
References
- [1] Gil, J. Werman, M., Computing 2-D min, median, and max filters, IEEE Transactions on Pattern Analysis and Machine Intelligence, 15, 504-507, 1993
