4. Model-based dithering

So far all dithering methods have relied on the assumption that carefully positioned black and white pixels gave the illusion of greyscales, but we have not stated exactly how the human eye reacted. Also, we do not have an automated way to compare the results of two different algorithms: judging that an algorithm is “better” has mostly been a subjective process so far.

In order to figure out what the human eye really sees, we need a human visual system (HVS) model. Countless models exist, and we are only going to focus on simple ones for now.

4.1. Gaussian human visual system model

One of the simplest models is the gaussian HVS model. It states that the human eye acts like a gaussian convolution filter, slightly blurring pixel neighbourhoods and therefore simulating what the eye sees as distance from the image increases. This model, a simplified luminance spatial frequency response formula, can be expressed using the two-dimensional exp(-(x²+y²)/2σ²) function. The σ parameter sort of introduces the viewing distance into the model.

Here are the results of applying a gaussian HVS to an 8×8 Bayer dithered image, simply by convoluting the image with a gaussian blur filter. This process is also known as inverse halftoning. Different values of σ simulate what the eye sees from different distances. On the left σ = 1, on the right σ = 2:

8×8 Bayer dither, gaussian HVS, σ = 1 8×8 Bayer dither, gaussian HVS, σ = 1 gradient 8×8 Bayer dither, gaussian HVS, σ = 2 8×8 Bayer dither, gaussian HVS, σ = 2 gradient

4.2. Direct binary search

We have already seen that standard error diffusion methods do not go back to pixels that have been set. Direct binary search [4] (DBS) is an iterative method that processes the image a fixed number of times, or until the error can no longer be minimised:

  • Generate an initial dithered image
  • Repeat until no changes can be applied:
    • Compute the global error between the original and the dithered images
    • For each pixel in the dithered image:
      • Compute the effect on the error of toggling the value of the current pixel
      • Compute the effect on the error of swapping the current pixel with one of its immediate neighbours
      • If the error can be reduced, perform the corresponding action

The efficiency and quality of DBS depend on many implementation details, starting with the HVS model it uses to compute the error. Also, the initial image used as iteration zero will give poor results if pattern artifacts are already present. The order in which pixels are processed is important, too. Unfortunately, despite its very high-quality results, DBS is usually a very slow algorithm.

Below is an example of the algorithm results. The HVS uses a 11×11 convolution kernel of the e<small><sup> -sqrt(x²+y²)</sup></small> function. The initial image is randomly thresholded, and pixels are processed in raster order. Iterations 1, 2 and 5 are shown:

direct binary search, iteration 0 direct binary search, iteration 0 gradient direct binary search, iteration 1 direct binary search, iteration 1 gradient

direct binary search, iteration 2 direct binary search, iteration 2 gradient direct binary search, iteration 5 direct binary search, iteration 5 gradient

Other HVS models can be used, giving very high quality results. Below are the results of DBS with the following HVS functions:

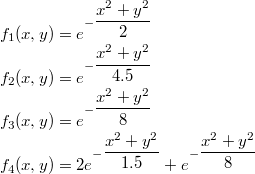
$f_1(x,y) = e^{-\dfrac{x^2+y^2}{2}}$ $f_2(x,y) = e^{-\dfrac{x^2+y^2}{4.5}}$ $f_3(x,y) = e^{-\dfrac{x^2+y^2}{8}}$ $f_4(x,y) = 2e^{-\dfrac{x^2+y^2}{1.5}} + e^{-\dfrac{x^2+y^2}{8}}$

The iteration shown is number 5. More iterations would have improved the results even slightly more, but that would have been at the expense of performance:

direct binary search, sigma = 1, iteration 5 direct binary search, sigma = 1, iteration 5 gradient direct binary search, sigma = 1.5, iteration 5 direct binary search, sigma = 1.5, iteration 5 gradient

direct binary search, sigma = 2, iteration 5 direct binary search, sigma = 2, iteration 5 gradient direct binary search, best HVS, iteration 5 direct binary search, best HVS, iteration 5 gradient

4.3 Comparing dithering algorithms

Using an HVS model, it is possible to classify previously seen algorithms simply by applying the model to both the source and the destination images, and computing their per-pixel mean squared error. This gives a better estimation of the dithering algorithm’s quality than simply computing a local, pixel-bound error.

The following table shows that different HVS models give very different error values depending on the value of σ. Also, in the case of the DBS algorithm, a carefully crafted HVS function such as the last one, which combines two different HVS models, gives low error values at every σ, which means the dithered image is close to the original image at all corresponding viewing distances:

Chapter 1: Thresholding Error %
σ = 1		Error %
σ = 1.5		Error %
σ = 2
0.5 thresholding 8.603037.935547.42669
0.4 thresholding 9.789909.109948.61878
0.6 thresholding 10.7768910.3337310.00462
dynamic thresholding 10.315689.607499.09760
uniform random dithering 1.578950.697620.39713
gaussian random dithering 2.955902.344612.08792
Chapter 2: Halftoning Error %
σ = 1		Error %
σ = 1.5		Error %
σ = 2
25/50/75% patterns dithering 0.566420.464900.41816
2×2 Bayer dithering 0.566940.466220.41956
4×4 Bayer dithering 0.205380.080600.05457
8×8 Bayer dithering 0.196910.063520.03354
4×4 cluster dot dithering 1.200260.148630.07100
8×8 cluster dot dithering 3.862360.852360.14443
5×3 artistic line dithering 2.755900.494200.11578
perturbated 8×8 Bayer dithering 0.405500.169710.09804
random 3×3 dithering matrix selection 0.603290.250550.16521
“plus” pattern dithering 0.430610.335400.29851
“hex” pattern dithering 0.267470.161190.13068
“doubleplus” pattern dithering 0.428520.122320.08904
“hex2” pattern dithering 0.350570.130460.09533
4-wise supercell “plus” pattern dithering 0.219030.074940.04423
3-wise supercell “hex” pattern dithering 0.216210.073560.04193
4-wise supercell “doubleplus” pattern dithering 0.408830.070510.03609
6th order dragon curve dithering 0.205030.067190.03539
3-wise supercell “hex2” pattern dithering 0.326430.078610.04061
9-wise supercell “hex2” pattern dithering 0.323360.077750.04087
14×14 void-and-cluster dithering 0.197260.067480.03663
25×25 void-and-cluster dithering 0.192480.062670.03325
Chapter 3: Error diffusion Error %
σ = 1		Error %
σ = 1.5		Error %
σ = 2
naïve error diffusion 0.333520.063720.01961
Floyd-Steinberg error diffusion 0.092490.018470.00859
serpentine Floyd-Steinberg error diffusion 0.098910.018490.00749
Jarvis, Judice and Ninke dithering 0.271980.062570.03472
Fan dithering 0.102200.017280.00705
4-cell Shiau-Fan dithering 0.116180.017850.00660
5-cell Shiau-Fan dithering 0.115500.019500.00708
Stucki dithering 0.197650.053730.03012
Burkes dithering 0.158310.040140.02178
Sierra dithering 0.234980.054150.03011
Sierra 2 dithering 0.222490.051210.02812
Filter Lite 0.097400.016050.00638
Atkinson dithering 0.472090.310120.27339
Riemersma dithering on a Hilbert curve 0.282240.065290.02693
Riemersma dithering on a Hilbert 2 curve 0.266220.060030.02492
spatial Hilbert dithering on a Hilbert curve 0.272890.061240.02184
spatial Hilbert dithering on a Hilbert 2 curve 0.228210.052460.01911
dot diffusion 0.383010.080630.01918
dot diffusion with sharpen = 0.9 0.785460.349410.23479
dot diffusion with sharpen = 0.9 and zeta = 0.2 2.912872.193981.99858
serpentine Floyd-Steinberg with sharpen = 0.9 0.626150.308510.22111
omni-directional error diffusion 0.238600.068210.03498
Ostromoukhov’s variable error diffusion 0.112030.017720.00593
nearest block matching with 2×2 line tiles 1.924301.348221.13685
block error diffusion with 2×2 line tiles 0.868070.224110.08901
block error diffusion with 3×3 artistic tiles 1.786260.569570.23000
block error diffusion with all 2×2 tiles 0.564660.159100.06946
block error diffusion with all 2×2 tiles and
weighted intra-block error distribution		 0.377380.104340.04643
sub-block error diffusion with all 2×2 tiles 0.146970.026050.00894
sub-block error diffusion with 2×2 line tiles 0.357590.060810.01855
sub-block error diffusion with all 3×3 tiles 0.328020.065160.02165
sub-block error diffusion with 3×3 artistic tiles 1.039630.218390.06678
Chapter 4: Model-based dithering Error %
σ = 1		Error %
σ = 1.5		Error %
σ = 2
DBS with HVS e -sqrt(x²+y²), iteration 1 0.258100.067800.03489
DBS with HVS e -sqrt(x²+y²), iteration 2 0.137620.032340.01939
DBS with HVS e -sqrt(x²+y²), iteration 5 0.104520.027450.01918
DBS with HVS e -(x²+y²)/2, iteration 5 0.103440.038600.02669
DBS with HVS e -(x²+y²)/4.5, iteration 5 0.180340.009840.00219
DBS with HVS e -(x²+y²)/8, iteration 5 0.378040.028660.00295
DBS with HVS 2e -(x²+y²)/1.5 + e -(x²+y²)/8, iteration 5 0.098380.008840.00263
Last modified 15 years ago Last modified on 12/22/2009 09:19:36 PM