About img2twit
img2twit is a program that reads an image and compresses it to a short string of text. It can be used, eg. on Twitter.
The first I read about this problem was here.
There is now a competition on StackOverflow.com.
Preliminary results
Here are the results of img2twit using 140 characters, restricted to U+4e00..U+9fa5 (CJK Unified Ideographs).
漙嬏阁勈麸疩虡渃痈魀掄鉿銐琭眇砷痂獰撿劚唯籤劈鋤熈磛冧仾炙渤勾糣鲁欚輓笏鵙岩恃陶穮嵨攚瞑譁犝倦觋夓圦皮焹鴉丱婿窌疳豄杀瘫籖喗裭攉觳滊僸鈞繽妑萢堛仭滇糚鈡罁端渭闧鳌垜徜嗙梾偞窓霤貊晦沺会琑顚霖鉽圊櫹妎厁膲乘鍌厔茢絜鳣嬥薽魘醙叡褒遠磁鉧糬冐浲仠砙娫贫玃纵吀恙黥鈴绐陑摢聙詁棥醩佟鯩岳孟
苉憗揣嶕繠剳腏篮濕茝霮墧蒆棌杚蓳縳樟赒肴飗噹砃燋任朓峂釰靂陴貜犟掝喗讄荛砙矺敨鷾瓔亨髎芟氲簵鸬嫤鉸俇激躙憮鄴甮槺骳佛愚猪駪惾嫥綖珏矯坼堭颽箽赭飉訥偁箝窂蹻熛漧衆橼愀航玴毡裋頢羔恺墎嬔鑹楄瑥鶼呍蕖抲鸝秓苾绒酯嵞脔婺污囉酼俵菛琪棺则辩曚鸸職銛蒝礭鱚蟺稿纡醾陴鳣尥蟀惘鋁髚忩祤脤养趯沅况
瓊锧抹璧浀飈捤賊麶橎紼杲籯愕勷剷棡苇緀峾烄寊倧塵湈嬅柮掯蠥揓趫龋鴥灭頃挨鸃鵱衂滟衏媵櫝篢贬塣劙捍蕼綕薿拨镶貶石聫艻綷蚸爫穧狜贮鶗迀祬貅缈宏鬽尜畳谬呏硫炟铹穜奫袧蹬虜藯趵螬壐挴钺佁莣厭嬋尯孀朢紈匝掸拰晳询铳矾放誃碠鱽閦娮諒懹覊噡綆结酯嘴謱嶔驃弟锯膇黮藒杏稿拎诽倸贜别盬竈浈璝锉橪欘一
蜥秓鋖筷聝诿缰偺腶漷庯祩皙靊谪獜岨幻寤厎趆脘搇梄踥桻理戂溥欇渹裏軱骿苸髙骟市簶璨粭浧鱉捕弫潮衍蚙瀹岚玧霫鏓蓕戲債鼶襋躻弯袮足庭侅旍凼飙驅據嘛掔倾诗籂阉嶹婻椿糢墤渽緛赐更儅棫武婩縑逡荨璙杯翉珸齸陁颗鳣憫擲舥攩寉鈶兓庭璱篂鰀乾丕耓庁錸努樀肝亖弜喆蝞躐葌熲谎蛪曟暙刍镶媏嘝驌慸盂氤缰殾譑
豪弅淶鑆斳愔耐俬秱戂孤访红艶劃嬌躑擣昗呎腆猎扭僬题猛嬰頽恓劉檭橀韮闼帣赑峈鮦宝鰢斣麙蓑騰騺鹸希關鈯穨唖秴斮圫究傲駛朘铃邂巢沿譓船櫃晒峩泪蝻鵲皲販口谹鎺侒戣耔凉蠛抏槱戛蝂荄勞攞咉闏涪彃沏全偫吒溸乎洸螕慹鳩弭蚕弣寽砰薨埻铥恣噿悏镏雈壭蒬礡靑徠鼛慗泏郄渺婥俦攨賌羢髙壶耔僪爯姉蔮蠬伣豖弫
Comparing to other algorithms
On the left, Mona Lisa scaled down and compressed to 536 bytes (4288 bits) using aggressive JPEG compression. On the right, Mona Lisa compressed by img2twit to 4287 bits.
Getting img2twit
You can use img2twit, modify it and redistribute it for any purpose, according to the terms of the WTFPL. Note however that it uses third-party libraries such CGAL (which has odd licensing terms) and Imlib2.
img2twit is currently research material and is not available in any released software yet. If you wish to try it, get the libpipi source code.
If you just want to have a look at the code, get it from the web-based browser.
How it works
My goal is to reach a reasonable compromise between the following:
- Fast decompression (a fraction of a second)
- Reasonable compression time (around 1 minute for high quality)
- Achieve decent reconstruction quality
- Work with various message length and character sets
- Do not waste a single bit of information
Here is a rough overview of the encoding process:
- The number of available bits is computed from desired message length and usable charset
- The source image is segmented into as many square cells as the available bits permit
- A fixed number of points (currently 2) is affected to each cell, with initial coordinates and colour values
- The following is repeated until a quality condition is met:
- A point is chosen a random
- An operation is performed at random on this point (moving it inside its cell, changing its colour)
- If the resulting image (see the decoding process below) is closer to the source image, the operation is kept
- The image size and list of points is encoded in UTF-8
And this is the decoding process:
- The image size and points are read from the UTF-8 stream
- For each pixel in the destination image:
- The list of natural neigbours is computed
- The pixel's final colour is set as a weighted average of its natural neighbours' colours
Bit allocation
UTF-8 is restricted to the formal Unicode definition by RFC 3629, meaning that once the 2¹¹ high and low surrogates and the 66 non-characters are removed from the U+0000..U+10FFFF range, the final size of the UTF-8 character set is 1111998. However, a lot of these characters are undefined, not yet allocated or are control characters. As of Unicode 5.1 there are only 100507 graphic characters.
The number of bits that can be expressed in a 140-character message using this charset is:
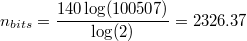
If we restrict ourselves to the 20902 characters available in the CJK Unified Ideographs block, the number of bits becomes:
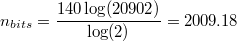
And finally, using the 94 non-spacing, printable ASCII characters:
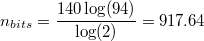
Optimised bitstream
There is a common misconception that values in an information stream should be bit-aligned. This is not the case at all in img2twit: the bitstream can store integer values with non-power of two bounds.
As an illustration, take the example of 16-bit colour coding. There are basically two widespread ways of storing RGB data into a 16-bit word: either using 5 bits per component and wasting the last bit, or using 6 bits for the G value, because the human eye is more sensible to variations of green. The RGB triplet is then computed as (((R) * 64 + G) * 32 + B), and eg. the green value is retrieved as (RGB / 32) % 64. Though 5-6-5 looks rather balanced, that's actually 32 values of red, 64 values of green and 32 values of blue: twice as many values of green... is this really required?
In this case, img2twit's approach would be to use 40 values for each component, where the RGB triplet is computed as (((R) * 40 + G) * 40 + B), and eg. the green value is retrieved as (RGB / 40) % 40. This makes the computations a lot slower (modulo 64 is just a bit shift, while modulo 40 requires dividing the whole bitstream by 40). However, it offers better packing and a lot more control over the data representation. For instance, I found that 2 bits (4 values) per colour component was not enough, but that 3 bits (8 values) was more than required. I went for 6 values (2.58 bits). (Sidenote: in fact, in order to cram even more information into the 16 bits, it would use 39/48/35 in this particular case.)
One drawback is that this makes the bitstream completely unable to recover from bit corruption. However, for such small streams I don't care at all.
Point selection
I use 16 values for the X and Y position of a point within a cell, and 6 values for each R, G and B component. This uses roughly 15.755 bits. There is a way to reduce this value down to 15.252 bits by accounting for the fact that two points within a cell are interchangeable, but I have not yet found an elegant way to remove the duplicate information without butchering a lot of code.
However, what the algorithm does is try to use any extra bits at the end by increasing the G component. If this succeeds, it tries to increase the B component, and so on. Using this technique, one can be sure that no more than 13 bits are wasted.
Algorithm seed
For the algorithm to converge quickly, the initial image needs to be as close as possible to an ideal solution. Of course the method works correctly with an initial random seed, but since the fitting is very slow, it can take 2 to 3 times as long to converge to the same solution.
My current approach is to look at the current cell's brightest and darkest pixels, and to set the two initial points at these locations. There is a lot to be improved in this domain.
Image rendering
The final image is simply an interpolation of the control points stored in the image. I use natural neighbour interpolation because it is reasonably fast (remember that the main algorithm loop computes the effects of modifying control points, and thus require at least a partial render).
The rendering method is responsible for both the artifacts (mainly the embossed dots) and the nice edges found in some parts of the resulting images.
Attachments (12)
- lena_std_scaled.png (115.7 KB) - added by 17 years ago.
- Mona_Lisa_scaled.jpg (29.4 KB) - added by 17 years ago.
- so-logo.png (9.6 KB) - added by 17 years ago.
- mandrill_scaled.jpg (12.2 KB) - added by 17 years ago.
- Cornell_box_scaled.png (45.6 KB) - added by 17 years ago.
- twitter3.png (71.5 KB) - added by 17 years ago.
- twitter5.png (78.8 KB) - added by 17 years ago.
- minimona.jpg (536 bytes) - added by 17 years ago.
- minimona2.png (15.0 KB) - added by 17 years ago.
- twitter1.png (79.9 KB) - added by 17 years ago.
- twitter2.png (103.5 KB) - added by 17 years ago.
- twitter4.png (20.0 KB) - added by 17 years ago.
Download all attachments as: .zip












