Version 4 (modified by Sam Hocevar, 17 years ago) (diff)

--

Numbering tiles

If we want a straightforward way to linearly index tiles without necessarily knowing the image size, we can use the following enumeration:

0 1 3 6 10 15 21
2 4 7 11 16 22 29
5 8 12 17 23 30 38
9 13 18 24 31 39 …
14 19 25 32 40 …
20 26 33 41 …
27 34 42 …

One way to generate these values is using the Cantor polynomial:

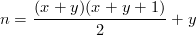
$n = \dfrac{(x + y) (x + y + 1)}{2} + y$

Efficiently inverting that polynomial is not trivial. Here is one way to do it:

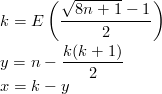
$k = E\left(\dfrac{\sqrt{8n+1}-1}{2}\right)$ $y = n - \dfrac{k (k + 1)}{2}$ $x = k - y$

The following C code works OK for values up to 10,000 (higher values may cause overflows), which potentially allows for procedural terapixel images. 

for(int y = 0; y < 10000; y++)
    for(int x = 0; x < 10000; x++)
    {
        int n = (x + y) * (x + y + 1) / 2 + y;
        int k = (sqrt((double)(n * 8 + 1)) - 1) / 2;
        int y2 = n - k * (k + 1) / 2;
        int x2 = k - y2;
        if(x != x2 || y != y2)
            printf("ERROR! %i %i -> %i -> %i %i\n", x, y, n, x2, y2);
    }