
Warning: this document is still work in progress. Feel free to send comments but do not consider it final material.
Dithering colour images means dithering three-dimensional elements (RGB pixels) instead of one-dimensional grey values. It is very complex and depends on the output media even more than greyscale dithering.
In some cases it is possible to perform three one-dimensional dithering operations instead of one three-dimensional one. Consider for instance the following palette:

It is made of the eight possible red/green/blue combinations made of 0 and 1 values:
| Red | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Green | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Blue | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
One way of dithering an image using this palette is to convert the image into three greyscale images (separating the red, green and blue channels), dither each subimage to two colours separately and recombine the images into three channels. For instance, if at a given pixel the red channel is dithered to 1 and the green and blue channels are dithered to 0, the final pixel will be [1 0 0] which is the colour red.
Separate-space dithering works by splitting the image into three red, green and blue channels. Each of this channel is treated as a greyscale image that is then dithered to black and white using any dithering method seen previously. The resulting images are then treated again as three red, green and blue channels and recombined into the final image:

Here are the results with serpentine Floyd-Steinberg dithering applied to each channel. On the left, no colour correction, as The Gimp or Photoshop would do; on the right, gamma-corrected dithering:
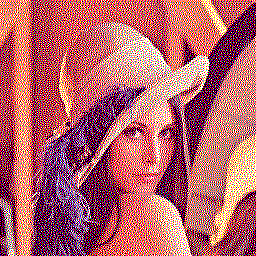

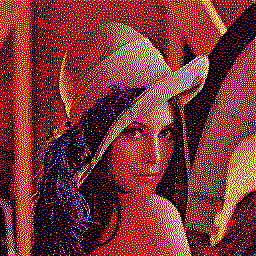

The previous palette was suitable for separate-space dithering. Such a palette is called separable or orthogonal.
Here is a palette that cannot be used in the same way:

As can be seen, it does not have the [0.5 0.5 0.5] grey colour, or the [1 0.5 0] orange colour, for instance, despite having other combinations of 0, 0.5 and 1 values:
| Red | 0 | 0 | 0.5 | 0.5 | 0 | 0 | 0.5 | 0.7 | 0.3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Green | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.5 | 0.7 | 0.3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Blue | 0 | 0.5 | 0 | 0.5 | 0 | 0.5 | 0 | 0.7 | 0.3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
It is no longer possible to compute the closest colour in each colourspace and combine them into an RGB colour, since that colour might not be available in the palette. So we need to determine what the “closest colour” means when dealing with the whole colour spectrum.
The following examples show gamma-corrected Floyd-Steinberg using the above 16-colour palette and two different definitions of distance: the sum of absolute differences and the euclidian distance. The sum of absolute differences performs pretty poorly because it does not penalise wide disparities:




Distances can be computed in another space. For instance, the HSV space allows to give colour variations a smaller influence than brightness variations simply by changing the HSV cone’s height. On the left is spatial Floyd-Steinberg using the euclidian distance in an HSV cone of height 1 and base radius 1. On the right is the same distance within a cone of height 3 and base radius 1:


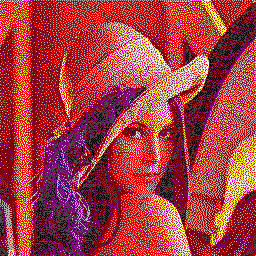

The following patterns show four ways to dither the same colour using our 8-colour palette:
All patterns visually blend to the same shade, but the last one is the most visually appealing:

Shaked, Arad, Fitzhugh and Sobel introduce the minimum brightness variation criterion (MBVC), stating that in order to reduce halftone noise, the halftone set which should be used to render the desired colour should be the one whose brightness variation is minimal [25]. Similarly, Klassen et al. suggest the selection of low-contrast colour combiation wherever possible [24].
Adapting sub-block error diffusion to colour images is almost straightforward. The major problem is proper weighting in the block-choosing step. It is a crucial part of the algorithm, and we have yet to find an efficient method to perform it.
The images below shows the result using our now well-known “lines” tile list, using respectively the 8-colour palette and the 16-colour palette:
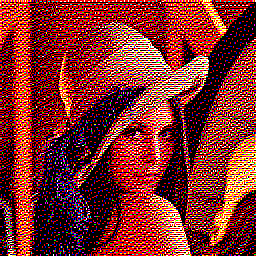


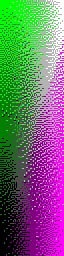
Speed is starting to become a problematic issue. A 16-colour palette can generate 65,536 unique 2×2 blocks. Exhaustive search to determine the best tile is no longer realistic, and we need to find better ways to find the best matching block.