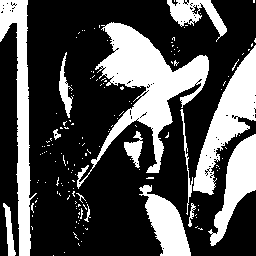
Warning: this document is still work in progress. Feel free to send comments but do not consider it final material.

1. Colour quantisation

The process of reducing the number of colours used in an image is called colour quantisation. It is a very old and common computer graphics problem. Many methods exist to do the task, and their efficiency depends on several parameters:

• the input image: is it a photograph? a vector drawing? a composition of both?
• the target media: is it a computer screen? if so, what are the size and the position of the pixels? is it a printed document? if so, what kind of paper? what kind of ink? or maybe the conversion should be optimised for both targets?
• the quality requirements: for instance, can contrast be raised for a more appealing result at the expense of accuracy?
• the allowed computation time: do we need 50fps or can we afford to wait 10 seconds for a better result?

1.1. Black and white thresholding

Since a greyscale pixel has a value between 0 and 1, a fast method to convert the image to black and white is to set all pixels below 0.5 to black and all pixels above 0.5 to white. This method is called thresholding and, in our case, results in the following image:

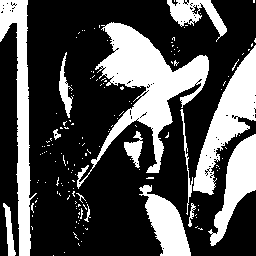
Not that bad, but we were pretty lucky: the original image’s brightness was rather well balanced. A lot of detail is lost, though. Different results can be obtained by choosing “threshold values” other than 0.5, for instance 0.4 or 0.6, resulting in a much brighter or darker image:

Choosing the best thresholding value for a given image is called average dithering. But even with the best value, the results will not improve tremendously.

1.2. Greyscale thresholding

Better results can be achieved with a slightly bigger palette. Here is thresholding applied to a 3-colour and to a 5-colour palette:

Using this method, shades of grey are evenly used. However, the global error is far from optimal, as the following graphs show:

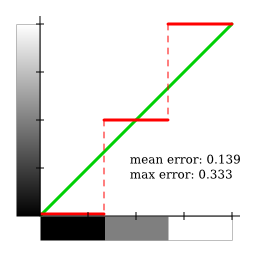
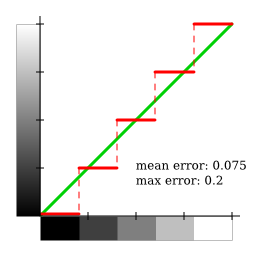
The following thresholding method minimises the error, at the cost of underusage of pure black and white colours:

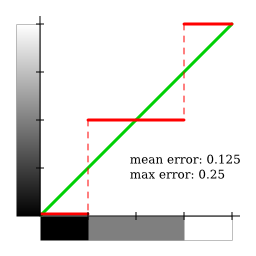
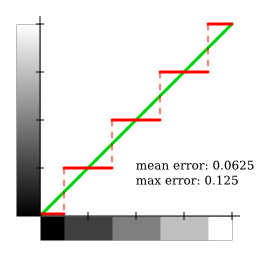
This is a perfect example of a situation where colour accuracy does not help achieve a better result.

1.3. Dynamic thresholding

Dynamic thresholding consists in studying the image before selecting the threshold values. One strategy, for instance, is to choose the median pixel value. This is done simply by computing a histogram of the image.

1.4. Random dithering

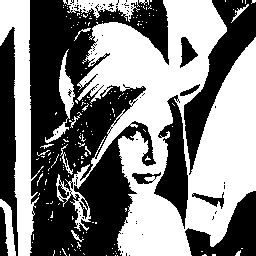
Instead of constantly using the same threshold value, one can use a different random value for each pixel in the image. This technique is simply called random dithering.

Here are two simple examples. On the left, threshold values are uniformly chosen between 0 and 1. On the right, random dithering with threshold values chosen with a gaussian distribution (mean 0.5, standard deviation 0.15):

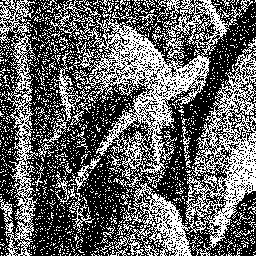
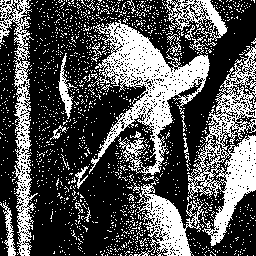
The images look very noisy, but they are arguably an improvement over standard constant thresholding.

Finally, this is dynamic thresholding with 4 colours where threshold values at every pixel are computed as usual, but then perturbated using a gaussian distribution (mean 0, standard deviation 0.08):